بطور کلی روش حساب تغییرات به مساله غیر خطی با شرایط حدی در دو نقطه مجزا منتهی می شود که برای بدست آوردن قانون کنترل بهینه و یا حتی یک کنترل بهینه حلقه باز نمی تواند بصورت تحلیلی حل شود.
برای حل عددی مسایل کنترل بهینه با شرایط مرزی در دو نقطه مجزا باید از روشهای عددی کمک گرفت. در این پست چهار روش عددی به منظور تعیین کنترلر بهینه و همچنین منحنی مسیرهای بهینه برای یک سیستم غیرخطی بکار گرفته می شود. این روشها عبارتند از:
- سریعترین سقوط (Steepest Descent)
- تغییر نهایتها (Variation of Extremals)
- خطی کردن مجازی (Quasilinearization)
- گرادیان تصویر (Projection Gradient)
این روش ها بعنوان مثال در کتاب کنترل بهینه کرک (kirk) در فصل ششم کتاب بیان شده اند. شما میتوانید کد متلب این چهار مثال را همراه با یک گزارش ورد از قسمت زیر دانلود بفرمایید
محتویات دانلود:
- کد متلب مثال 6.2.2
- گزارش
- کد متلب مثال 6.3.2
- گزارش
- کد متلب مثال 6.4.3
- گزارش
- کد متلب مثال 6.6.2
- گزارش
- لینک دانلود فایل بلافاصله بعد از پرداخت وجه به نمایش در خواهد آمد.
- همچنین لینک دانلود به ایمیل شما ارسال خواهد شد به همین دلیل ایمیل خود را به دقت وارد نمایید.
- ممکن است ایمیل ارسالی به پوشه اسپم یا Bulk ایمیل شما ارسال شده باشد.
- در صورتی که به هر دلیلی موفق به دانلود فایل مورد نظر نشدید با ما تماس بگیرید.
 مرجع مهندسی كنترل | دانش با کیفیت در مرز علم
مرجع مهندسی كنترل | دانش با کیفیت در مرز علم



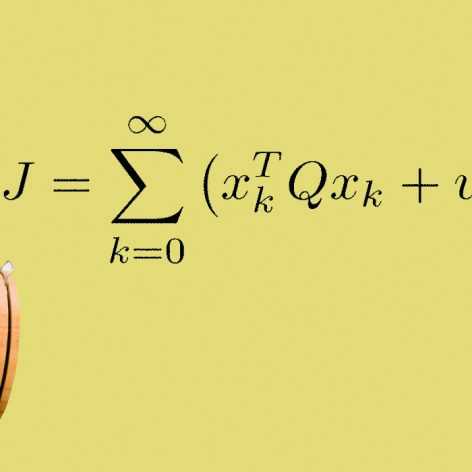



نقد و بررسیها
هنوز بررسیای ثبت نشده است.