کنترل مقاوم به دلیل کاربردهای خیلی زیاد یکی از حوزه های مهم در تئوری کنترل محسوب میشود. عموما وقتی صحبت از کنترل مقاوم میشود همه به یاد ∞H و LFT و کلی ریاضیات پیچیده مثل تعریف نرم ها و فضاهای علمی تخیلی دیگر (مثل فضای هاردی) میافتند. وقتی بنده درس سه واحدی کنترل مقاوم را گذراندم، احساس کردم برای این کار باید راههای راحت تر و بهتری وجود داشته باشد! تا اینکه با LMI آشنا شدم و دیدم که چطور بعضی ها توانستهاند هر مساله کنترلی را به نامساوی ماتریسی خطی تبدیل کنند، از جمله حذف نامعینی و تضعیف اغتشاش. اگر نگاهی به مقالات 10-15 سال اخیر در زمینه کنترل بیندازید، خواهید دید که در اکثر موارد (کنترل مقاوم یا غیر مقاوم) از روش مستقیم لیاپونوف استفاده کرده و مساله پایداری را به LMI تبدیل میکنند. برای اینکه این تجربه را به شما هم انتقال بدهم، تصمیم گرفتم که روشهای بر مبنای LMI را برای مسایل مختلف کنترلی از قبیل حذف نامعینی؛ تضعیف اغتشاش؛ طراحی رویتگر و … به تدریج در سایت قرار بدهم. برای شروع، در این سری جلسات نحوه فرمولبندی مساله حذف نامعینی پارامتری را برای سیستمهای خطی به صورت LMI تقدیم میکنم. با امید به اینکه برای شما مفید واقع بشود.
پیشنیازها: آشنایی اولیه با جبر خطی و تئوری پایداری لیاپونوف – آشنایی با کدنویسی در محیط متلب – آشنایی با نامساویهای ماتریسی خطی (LMI)
قبل از دیدن ادامه پست، راهنمای استفاده از سری فیلمهای کنترل مقاوم را حتما ببینید:
جلسه اول:
معرفی مقدماتی کنترلکننده های مقاوم و انواع نامعینی ها
در این جلسه ابتدا برخی توضیحات کلی در مورد کنترل مقاوم ارایه شده و روشهای متفاوت موجود در این حوزه معرفی میشوند. همچنین مزایای استفاده از نامساویهای ماتریسی خطی برای حل مساله کنترل مقاوم نسبت به روشهای مرسوم مانند ∞H بیان میشود. در انتها انواع نامعینیها تعریف شده و روشهای مرسوم برای مدلسازی نامعینی بر اساس یک مقاله ISI معرفی میشود.
مدت زمان آموزش: 69 دقیقه
محتویات درس: فیلم با کیفیت 720p- پاورپوینت درس و مقاله های مورد اشاره در فیلم
حجم فایل: 145 مگابایت
پیش نمایش جلسه اول:
جلسه دوم:
طراحی کنترل کننده مقاوم به دو روش مقدار ویژه و روش مستقیم لیاپونوف برای یک سیستم اسکالر و شبیهسازی در متلب
در این جلسه ابتدا روشهای مختلف پایداری لیاپونوف معرفی شده و به صورت مختصر توضیح داده میشوند. سپس برای یک مثال اسکالر دارای نامعینی به دو روش مقدار ویژه و روش مستقیم لیاپونوف کنترل کننده مقاوم طراحی میشود. در انتها با کنترل کننده بدست آمده سیستم حلقه بسته در محیط متلب شبیهسازی میگردد.
مدت زمان آموزش: 55 دقیقه
محتویات درس: فیلم با کیفیت 720p- پاورپوینت درس و کد متلب مربوط به مثال
حجم فایل: 83 مگابایت
پیش نمایش جلسه دوم:
جلسه سوم:
استخراج LMI های مورد نیاز با استفاده از مکمل شور و تبدیل متجانس
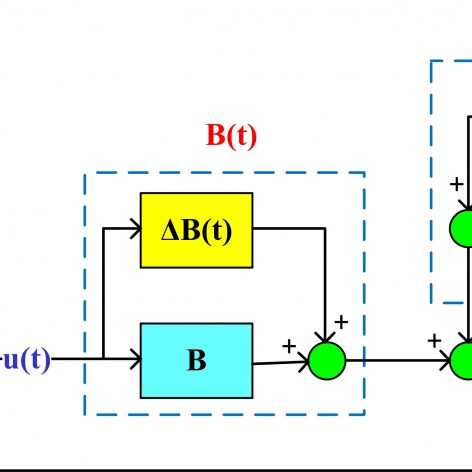
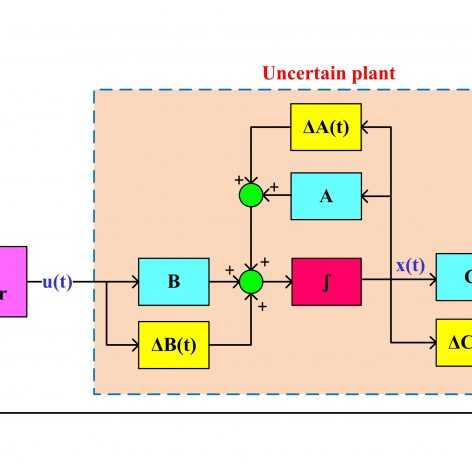
در این جلسه سیستمهای خطی با نامعینی پارامتری در حالت کلی در نظر گرفته شده و با استفاده از روش مستقیم لیاپونوف نحوه استخراج نامساوی ماتریسی خطی برای بدست آوردن بهره کنترل کننده فیدبک حالت تشریح میشود. سپس برای مثال اسکالر معرفی شده در جلسه دوم با حل LMI بدست آمده یک کنترل کننده مقاوم طراحی میشود.
مدت زمان آموزش: 77 دقیقه
محتویات درس: فیلم با کیفیت 720p- پاورپوینت درس- مقاله مورد اشاره در فیلم و کد متلب مربوط به مثال
حجم فایل: 106 مگابایت
پیش نمایش جلسه سوم:
جلسه چهارم:
مدلسازی نامعینی برای سیستم پاندول معکوس
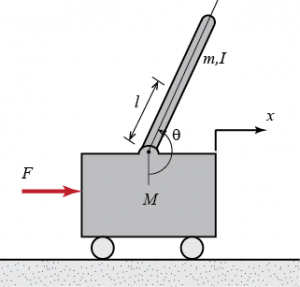
در این جلسه ابتدا دینامیک خطی پاندول معکوس معرفی میشود. با توجه به اهمیت مدلسازی نامعینی جهت طراحی کنترل کننده نحوه مدلسازی نامعینی به شکل استاندارد بیان شده در جلسات قبل برای سیستم پاندول معکوس تشریح میشود. برای سادگی مساله در این جلسه تنها یکی از پارامترهای پاندول معکوس نامعین در نظر گرفته میشود و نحوه مدلسازی این نامعینی روی ماتریسهای سیستم به تفصیل بررسی میشود.
مدت زمان آموزش: 64 دقیقه
محتویات درس: فیلم با کیفیت 720p و پاورپوینت درس
حجم فایل: 100 مگابایت
پیش نمایش جلسه چهارم:
جلسه پنجم:
پیادهسازی کنترلکننده مقاوم بر روی سیستم پاندول معکوس و شبیهسازی در متلب
در این جلسه الگوریتم مرحله به مرحله طراحی کنترل کننده مقاوم برای سیستمهای خطی با نامعینی پارامتری ارائه شده و برای حالتی که یکی از پارامترهای سیستم پاندول معکوس نامعین باشد. مدلسازی نامعینی در محیط متلب انجام شده و نامساوی ماتریسی خطی برای آن حل شده و بهره کنترل کننده فیدبک حالت مقاوم بدست آمده و سیستم حلقه بسته شبیهسازی میشود. در مرحله بعد فرض میشود که دو تا از پارامترهای سیستم پاندول معکوس نامعین بوده و همه مراحل قبل تکرار میشود. در تمامی حالتها عملکرد کنترل کننده فیدبک حالت مقاوم با یک کنترل کننده فیدبک حالت غیر مقاوم مقایسه شده و مقاومت کنترل کننده طراحی شده بررسی میشود. در انتها نحوه مدلسازی تعداد بیشتر پارامترها تشریح شده و دلایل احتمالی عدم حل پذیری نامساویهای ماتریسی خطی برای یک سیستم خاص و راه حلهای ممکن توضیح داده میشود. لازم به ذکر است که تمامی LMI ها با استفاده از تولباکس YALMIP در محیط متلب حل شده اند و بنابراین شما باید این تولباکس را قبل از اجرای کدها بر روی متلب نصب کرده باشید. برای توضیحات تکمیلی درباره نحوه دانلود و نصب تولباکس YALMIP به جلسه ششم از سری فیلمهای آموزش حل ناتساویهای ماتریسی خطی مراجعه فرمایید.
مدت زمان آموزش: 85 دقیقه
محتویات درس: فیلم با کیفیت 720p – پاورپوینت درس و کدهای متلب مربوط به طراحی و شبیهسازی
حجم فایل: 150 مگابایت
پیش نمایش جلسه پنجم:
جلسه ششم:
حل مساله ردیابی برای سیستمهای خطی دارای نامعینی پارامتری و اعمال به سیستم پاندول معکوس
در این جلسه بحث ردیابی سیستمهای خطی دارای نامعینی پارامتری به صورت کامل مورد بررسی قرار میگیرد. ابتدا قانون کلی استحصال ورودی کنترلی جهت ردیابی سیگنال مرجع معرفی شده و سپس با مثالهای متعدد و کاربردی نحوه بدست آوردن ساختار کنترل کننده جهت ردیابی سیستم به صورت گام به گام تشریح میشود. در انتها با همین شیوه کنترل کننده مورد نیاز برای ردیابی در سیستم پاندول معکوس که در جلسه پیش مساله رگولاسیون برای آن حل شد؛ طراحی شده و با شبیهسازی سیستم حلقه بسته در محیط m-file مورد ارزیابی قرار میگیرد.
مدت زمان آموزش: 81 دقیقه
محتویات درس: فیلم با کیفیت 720p – پاورپوینت درس و کدهای متلب مربوط به طراحی و شبیهسازی
حجم فایل: 124 مگابایت
پیش نمایش جلسه ششم:
۴۸۰,۰۰۰ تومان قیمت اصلی ۴۸۰,۰۰۰ تومان بود.۲۹۸,۸۰۰ تومانقیمت فعلی ۲۹۸,۸۰۰ تومان است.Add to cart
مطالعه بیشتر
 مرجع مهندسی كنترل | دانش با کیفیت در مرز علم
مرجع مهندسی كنترل | دانش با کیفیت در مرز علم






الیاس
سلام، خسته نباشید آقای دکتر.
اگر پلنت، کنترل پذیر نباشد، منظور این است که فقط با کنترل کننده استاتیکی قابل کنترل نیست یا با کنترل کننده های دیگر هم قابل کنترل نیست؟
پیشاپیش سپاسگزارم از شما
دکتر علی جوادی
سلام
با هیچ کنترل کننده ای قابل کنترل نیست
اکبر
سلام
فرق فایل های 4 جلسه ای و 6 جلسه ای کنترل مقاوم شما چیست؟
بنظرم همپوشانی دارد!!
alij63@gmail.com
سلام
جلسات رو با دقت ببینید تفاوتشون رو متوجه میشید
reza
با سلام
آقای دکتر امکان دریافت مشاوره از طرف شما وجود دارد؟
بنده در حال کار بر روی یک مقاله ای هستم که برای حل LMI آن به دو مشکل اساسی برخورد کردم و تمامی فیلم های مربوط به LMI رو هم مشاهده کردم اما مشکلم برطرف نشد.
از طریق این صفحه نیز فکر نکنم که بتونم به پاسخ برسم.
ممنون
علی جوادی
اقدام شد
reza
با سلام
اگر در یک LMI ترانهاده یک متغیر تصمیم گیری در درایه ای دیگر از ماتریس LMI وجود داشته باشد چگونه باید مساله را حل نمود؟
به عنوان مثال :
[H’ F; H I]
علی جوادی
سلام
قسمت متقارنش رو برای حل استفاده کنید یعنی اگر ماتریس A نامتقارن رو دارید به جای خودش از 0.5*(A+A’) استفاده کنید
reza
سلام
ماتریس مربوط به متغیر تصمیم گیری مربعی نیست پس چطور میشه که با ترانهاده خودش جمع بشه؟
علی جوادی
ماتریسهای مربوط به LMI حتما باید مربعی باشند چون مثبت یا منفی معین بودن برای ماتریسهای مربعی تعریف میشه ولی متغیرهای تصمیم گیری به هر صورتی میتونند داخل LMI ظاهر شوند
zandi
سلام
این روش برای سیستم های که تعداد ورودی ها بیشتر از تعداد متغیر های حالت هست،نیز قابل حل است؟
اگر بخواهم قطب های حلقه بسته رو سریع تر کنم،چه تغییراتی باید به ماتریس اصلی اعمال کنم؟
با تشکر
علی جوادی
سلام
محدودیتی برای تعداد ورودیها و حالتها وجود نداره.
با روش ارائه شده نمیشه سیستم حلقه بسته رو سریعتر کرد. در واقع نیاز به تغییراتی در LMI هست که در این مجموعه تدریس نشده
یاسین
با سلام مجدد خدمت آقای دکتر جوادی و ممنون از آموزش بسیار خوبشان
آقای دکتر سایز ماتریس های من بزرگ هستند، بجای اعمال درایه به درایه آیا بطور ماتریسی می توان عدم قطعیت را مدل کرد؟ مثلا فرض کنید ماتریس جرم بصورت یک ماتریس قطری 11 در 11 باشد با مقادیر m1 تا m11 و یک ماتریس سختی و میرایی داشته باشیم که ماتریس های فول 11 در 11 هستند و ماتریس سیستم A یکی از درایه هایش بصورت inverse(m)*k هست که خودش یک ماتریس 11 در 11 هست که خود ماتریس جرم سیستم m از درایه های m1 تا m11 و ماتریس سختی سیستم از k1 تا k11 تشکیل شده و به شکل ماتریسی در ماتریس حالت سیستم A ظاهر می شوند. آیا روشی برای اعمال نامعینی به ماتریس جرم و سختی به شکل ماتریسی هست که نامعینی m1 تا m11 و نامعینی k1 تا k11 را بصورت ماتریسی اعمال کنه؟ چون تک به تک اعمال آنها با توجه به سایز بزرگ ماتریس حالت سیستم A زمانبر هست و حتی معکوس ماتریس جرم در ماتریس سختی در ماتریس حالت سیستم A ضرب شده است. خیلی ممنون میشم آقای دکتر در این مورد راهنمایی بفرمایید.
علی جوادی
تا جایی که من میدونم باید دستی مقادیر ماکزیمم و مینیمم پارامترها رو قرار بدید و باندهای نامعینی رو بدست بیارید
یاسین
با سلام و خسته نباشید خدمت آقای دکتر جوادی
آقای دکتر در ماتریس سیستم A اگر ما بطور مثال ماتریس جرم داشته باشیم که درایه های آن نامعین باشند مثلا m1 و m2 و m3 و اینها رو در قالب ماتریس M در ماتریس حالت سیستم A بیاریم و معکوس M هم در ماتریس A ظاهر میشه همین روش شما را برای اعمال عدم قطعیت به ماتریس جرم سیستم که سه تا جرم داره و معکوس این ماتریس هم در ماتریس A هست چطور می توان اعمال کرد؟ ممنون
علی جوادی
سلام
مهم نیست که هم جرم ظاهر شده و هم معکوسش. بالاخره هر درایه از ماتریس A یک مینیمم و ماکزیمم داره. کافیه مقادیر مینیمم و ماکزیمم جرمها رو در نظر بگیرید و باند نامعینی رو متناظر با این درایه ها بدست بیارید.