مرجع مهندسی كنترل | دانش با کیفیت در مرز علم
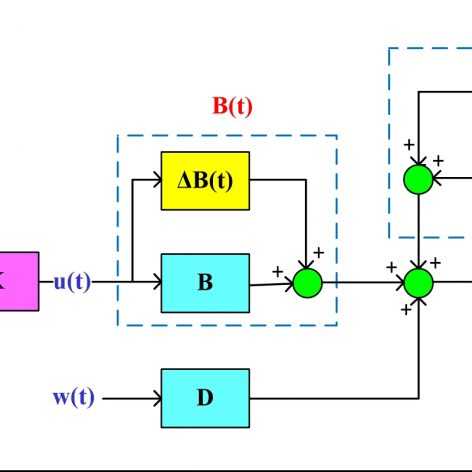
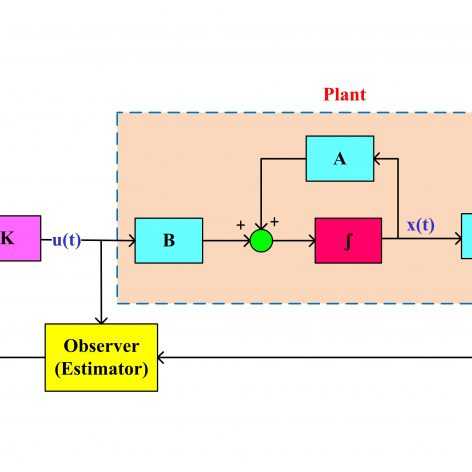
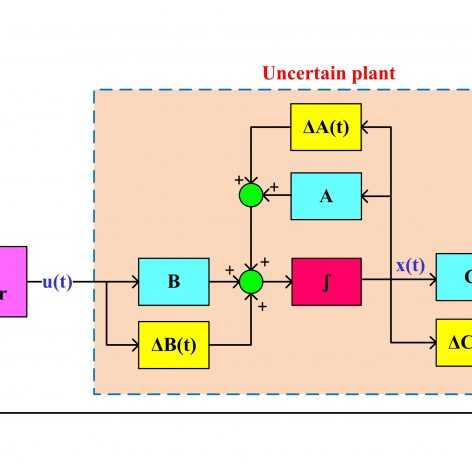
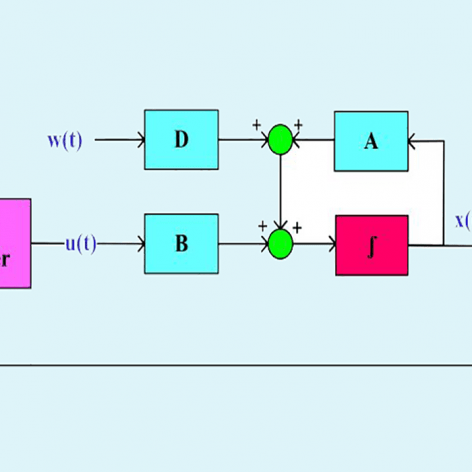
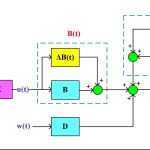
در سری فیلمهای قبلی موجود در سایت، کنترل مقاوم سیستمهای خطی تحت نامعینی پارامتری و کنترل مقاوم ∞H سیستمهای خطی دارای اغتشاش از طریق فیدبک حالت و با استفاده از نامساویهای ماتریسی خطی به صورت جداگانه مورد بررسی قرار گرفته و شروط LMI مورد نیاز برای هر دو مورد بدست آمد. خیلی از سیستمها به صورت همزمان تحت تأثیر نامعینی پارامتری و اغتشاش قرار دارند و بنابراین نمی‌توان از LMI های بدست آمده در سری فیلمهای فوق برای این سیستمها استفاده کرد. در این سری جلسات برای این سیستمها که کلی تر هم هستند، LMI های مورد نیاز برای بدست آوردن بهره کنترل کننده فیدبک حالت جهت حذف اثر نامعینی پارامتری و همچنین تضعیف اغتشاش محاسبه خواهند شد. برای نشان دادن عملکرد خوب این کنترل کننده روش پیشنهادی روی سیستم تعلیق فعال خودرو پیاده شده و با حالت غیر فعال مقایسه شده است. امیدوارم مورد توجه شما قرار بگیرد…
پیشنیازها: آشنایی اولیه با جبر خطی و تئوری پایداری لیاپونوف – آشنایی با کدنویسی در محیط متلب – آشنایی با نامساویهای ماتریسی خطی (LMI)
قبل از دیدن ادامه پست، راهنمای استفاده از سری فیلمهای کنترل مقاوم را حتما ببینید:
جلسه اول:
فرمولبندی طراحی کنترل مقاوم فیدبک حالت برای سیستمهای دارای اغتشاش خارجی و نامعینی پارامتری و استخراج LMI های مورد نیاز
جلسه دوم:
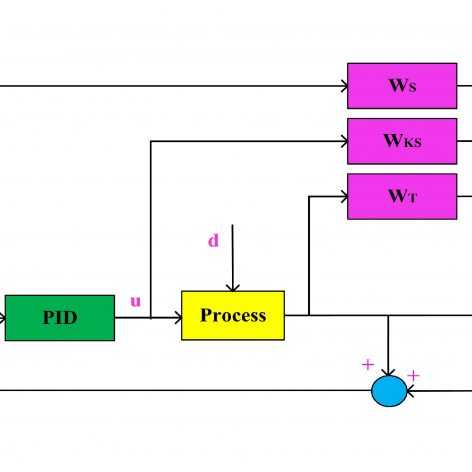
پیاده‌سازی کنترل‌کننده مقاوم بر روی سیستم تعلیق فعال خودرو و شبیه‌سازی در متلب
Original price was: ۲۰۴,۰۰۰ تومان.۱۱۶,۴۰۰ تومانCurrent price is: ۱۱۶,۴۰۰ تومان.Add to cart
- لینک دانلود فایل بلافاصله بعد از پرداخت وجه به نمایش در خواهد آمد.
- همچنین لینک دانلود به ایمیل شما ارسال خواهد شد به همین دلیل ایمیل خود را به دقت وارد نمایید.
- ممکن است ایمیل ارسالی به پوشه اسپم یا Bulk ایمیل شما ارسال شده باشد.
- در صورتی که به هر دلیلی موفق به دانلود فایل مورد نظر نشدید با ما تماس بگیرید.
مصطفي
آقاي دكتر جوادي سلام وقت جنابعالي بخير.
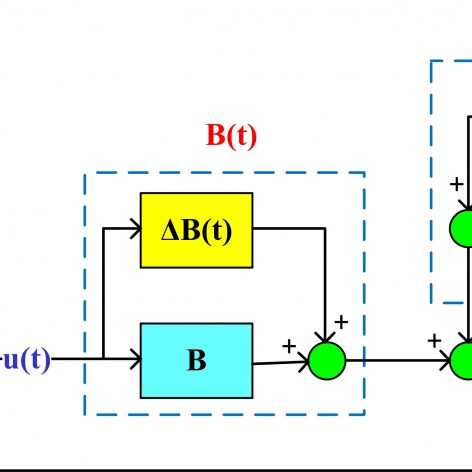
در مدل بنده هم نامعيني هست و هم اغتشاش ماتريس َA و C1 داراي نامعيني و ماتريس هاي ديگر بدون نامعينيند بعد از نوشتن LMI ها عليرغم اينكه مقدار گاما را حتي اعداد بسيار بزرگ انتخاب ميكنم منتهي نتايج اكي نميشند به نظر شما مشكل از چي ميتونه باشه؟
دکتر علی جوادی
سلام
دلایل خیلی زیادی میتونه داشته باشه مثلا اینکه نامعینی زیاد باشه یا کدنویسی مشکل داشته باشه یا سیستم کنترل پذیر نباشه و …
مصطفي
آقاي دكتر مجددا عذر بنده رابپذيريد. منظورم از اينكه نتايج اكي نميشه اينه كه ماترس هاي كنترل ديناميكي يعني Ah و Bh عدد هاي بزرگي به خود اختصاص مي دند. بنده از كد نويسيم مطمئن هستم مدل كنترل پذير هست و كلا دو كميت نا معيني دارم و اين نامعيني ها در ماتريس هاي A و C1 هست و ماتريس D12 صفر هست.
دکتر علی جوادی
در این روش تضمینی نیست که ماتریسها مقادیر کوچکی داشته باشند. اگر LMI ها فیزبل بشند، سیستم باید پایدار بشه ولی معلوم نیست ماتریسها بزرگ باشند یا کوچک
مصطفي
آقاي دكتر اميدوارم اين سوال آخر بنده باشه. در مدل من ورودي سيستم مشتق يكي از حالت هاست براي بحث رديابي قاعدتا ur برابر صفر ميشه. اينجا يك تناقض پيش مياد و اون هم اينكه براي رسيدن به يك خروجي مثلا yr ورودي نياز نيست رديابي اين گونه مسائل به چه صورتي هست ؟
دکتر علی جوادی
در اینحالت بهتره از انتگرال گیر استفاده کنید تا خروجی به مقدار مورد نظر برسه.
مصطفي
آقاي دكتر خيلي متشكرم. فقط فرموديد من يك انتگرال گير بين مدل و كنترل ديناميكي قرار بدم. از طرف ديگر در يكي از درساتون فرموديد مدل و كنترلر سنكرون هستند هر گونه تغيير در ساختار يكي در ديگري تاثير گذار هست آيا به نظرتون با قرار دادن اين انتگرال گير مشكلي ايجاد نميشه (با توجه به اينكه من LMI هارا بدون در نظر گرفتن اين انتگرال گير بدست آوردم).
دکتر علی جوادی
انتگرال گیر رو به مدل سیستم اضافه کنید و با حضور انتگرال گیر کنترل کننده طراحی کنید
جواد
با سلام و خسته نباشید.
آقای دکتر در مساله خودم بنده به این عبارت رسیدم مطابق با فیلم آموزشی، به چه نحوی میشه این عبارت رو به LMI تبدیل کرد؟
x*transpose(Nc1)*F(t)*transpose(Mc1)*MD11*F(t)*ND11
با تشکر
علی جوادی
سلام
تابع زمانی نباید داخل LMI حضور داشته باشه و باید به نحوی حذف بشه
فرزاد
سلام چرا کدهاتون که نوشتید با متلب ۲۰۱۸ ران میکنم روی عمگر sdpvar خطا میده و میگه ناشناس این عملگر ؟ الان من چکار کنم؟
علی جوادی
سلام
تولباکس Yalmip رو باید اول نصب کنید