عملکرد بسیاری از سیستمهای کاربردی تحت تاثیر نامعینی پارامترهای سیستم و اغتشاشات خارجی قرار دارد. از طرف دیگر در خیلی از سیستمها امکان اندازه‌گیری تمام حالتها وجود ندارد، چه به خاطر نبود سنسور مناسب و چه به خاطر هزینه بالای سنسورها. بنابراین اگر یک کنترل کننده بتواند با کمترین تعداد سنسور سیستم نامعین و تحت اغتشاش را کنترل کند، میتواند برای بهبود عملکرد بسیاری از سیستمها مورد استفاده قرار گیرد. تاکنون نحوه مواجهه با عوامل مخربی مانند اغتشاش خارجی و نامعینی جداگانه در سری فیلمهای مختلف موجود در سایت مورد بررسی قرار گرفته‌اند. به طور خاص فیلمهای آموزشی مربوط به کنترل سیستمهای خطی تحت نامعینی پارامتری و اغتشاش خارجی با فیدبک حالت؛ کنترل مقاوم سیستمهای خطی تحت نامعینی پارامتری با فیدبک خروجی و کنترل مقاوم ∞H سیستمهای خطی تحت نامعینی اغتشاش با فیدبک خروجی در سایت موجود هستند. در این سری جلسات قرار است همه این عوامل یکجا در نظر گرفته شده و سیستمهای خطی دارای نامعینی و اغتشاش تنها با فیدبک تعدادی از حالتها کنترل شود و نامساویهای مربوط به این مساله استخراج شود. یکی از مزایای این کنترل کننده این است که مثل رویتگر لیونبرگر نیازی به ورودی سیستم و استفاده مستقیم از ماتریسهای سیستم حلقه باز نداشته و فقط از خروجی سیستم استفاده میکند تا به اهداف مورد نظر برسد. البته کلیت این مساله نباید باعث شود که در تمام موارد از این روش استفاده شود؛ به خاطر اینکه ممکن است اثر نامعینی یا اغتشاش در یک سیستم خیلی کم بوده و قابل صرف نظر کردن باشد. بنابراین با توجه به اهمیت این عوامل و تعداد سنسورها می‌توان روش مناسب رو انتخاب کرد. برای جا افتادن مطلب، روش پیشنهادی روی یک مدل یک چهارم سیستم تعلیق هم پیاده شده و نتایج بدست آمده از کنترل کننده مقاوم با سناریوهای مختلف و تحت نامعینی ها و اغتشاشات متفاوت با نتایج سیستم کنترل تعلیق غیر فعال مقایسه می‌شود.
پیشنیازها: آشنایی اولیه با جبر خطی و تئوری پایداری لیاپونوف – آشنایی با کدنویسی در محیط متلب – آشنایی با نامساویهای ماتریسی خطی (LMI)
قبل از دیدن ادامه پست، راهنمای استفاده از سری فیلمهای کنترل مقاوم را حتما ببینید:
جلسه اول:
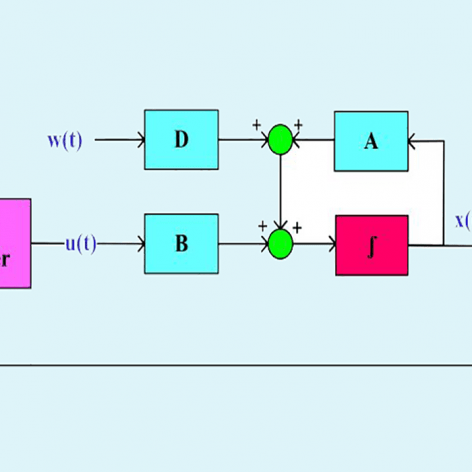
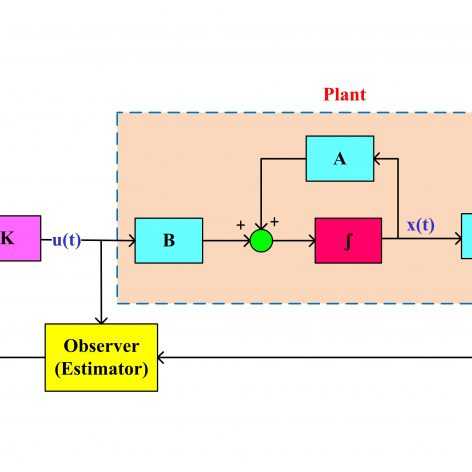
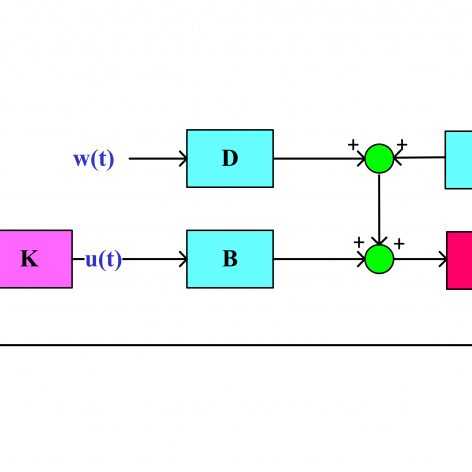
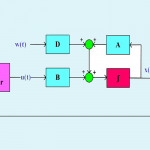
فرمولبندی طراحی کنترل مقاوم فیدبک خروجی برای سیستمهای دارای اغتشاش خارجی و نامعینی پارامتری
جلسه دوم:
استخراج LMI های مورد نیاز با استفاده از مکمل شور و تبدیل متجانس
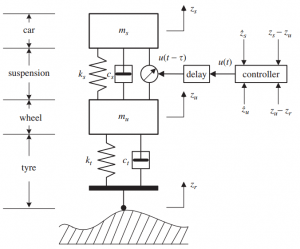
پیاده‌سازی کنترل‌کننده مقاوم بر روی سیستم تعلیق فعال خودرو و شبیه‌سازی در متلب
شبیه‌سازی در محیط سیمولینک و تحلیل در حوزه فرکانس
180,000 تومانافزودن به سبد خرید
جلسه سوم:
جلسه چهارم:
سلام، یک خلاصه از معادله دینامیکی سیستم بگذارید
سلام.
منظورتون رو متوجه نشدم. کدام معادله دینامیکی سیستم؟
سلام آقای دکتر. وقتتون بخیر.
اگر بعد از گذشت مثلا 1 ثانیه اغتشاش پله ای به سیستم وارد شود، در همان لحظه اول وارد شدن اغتشاش، سیگنال های حالت از سمت چپ مشتق پذیر نیستند.
از طرفی در سمت چپ معادلات حالت، ما مشتق سیگنال حالت را داریم، ولی در لحظه ورود اغتشاش سیگنال ها مشتق پذیر نیستند. این مساله را چگونه ارزیابی می نمایید؟
با تشکر
سلام
سوال رو نفهمیدم
عذرخواهم که خوب توضیح ندادم.
به طور واضح تر بخواهم بگویم:
سیستمی دارم که به آن اغتشاش پله ای بین بازه 1 و 4 ثانیه وارد شده است. وقتی حالت های سیستم را مشاهده می کنیم، در لحظه 1 و 4 مشتق پذیر نیستند. از طرفی در معادلات حالت، با مشتق سیگنال های حالت سر و کار داریم.
سوال این است که اگر نقاط مشتق ناپذیر در حالت های سیستم وجود داشته باشد، بنابراین معادلات حالت برای آن صادق نیست.
شما چگونه این مساله را ارزیابی می کنید؟
با سپاس
اولا مشتق پذیری رو تابع تعریف میشه نه روی حالت یا متغیر.
از طرفی دیگه تغییرات ناگهانی اغتشاش روی مشتق حالتها اثر میذاره نه روی خود حالتها
ممنونم بابت وقتی که گذاشتید.
سپاسگزارم از شما استاد گرانقدر
آقاي دكتر سلام و عرض ادب.
غرض از مزاحمت اينكه در مدلي كه بنده دارم دو تا ورودي وجود داره يكي ورودي خارجي و يكي ورودي كنترلر. ورودي خارجي هميشه يك عدد ثابت هست منتهي ميتونه تحت اغتشاش قرار بگيره بنده اين دو تا ورودي را به عنوان u (ورودي كنترلر و عدد ثابت ورودي خارجي) در نظر گرفتم و مقدار اغتشاشي كه ورودي خارجي ميتونه تحمل كنه را اغتشاش و w.طبق فرمايشات جنابعالي وقتي مدل كردم تو قسمت حل LMI، بعد از ران كردن خطا ميده :
All matrices on a row in the bracketed expression must have the same number of rows.
Error in kitedisturbance (line 145)
Cons=[ [R eye(nx);eye(nx) S] >=0]+..
علت اين خطا را كه بررسي كردم به نظر ميرسه كه قرار دادن ورودي خارجي و كنترلر در يك بردار مشكل ساز ميشه. عرض بنده اينه براي حل اين مشكل چه كاري بايدكرد؟ با تشكر از محبتتون
عرضم اينه آيا
سلام
من دقیقا نمیدونم منظورتون از ورودی خارجی چیه ولی تا جایی که فهمیدم ورودی خارجی تحت کنترل ما نیست بنابراین ورودی کنترلی حساب نمیشه.
در نتیجه ورودی خارجی میتونه به صورت اغتشاش در نظر گرفته بشه.
البته اغتشاشی که در روش H-infinity وجود داره نباید انرژی نامحدود داشته باشه (مثل همین حالتی که اغتشاش مقدار ثابت باشه) بنابراین اگر این ورودی خارجی رو اغتشاش هم در نظر بگیرید باز نمیشه از روش H-infinity استفاده کرد.
اصولا باید از روشهای دیگر اثر این نوع اغتشاش حذف بشه که البته من روش سیستماتیک برای این حالتها رو نمیشناسم و باید ببینید در مراجع چیکار میکنند
سلام آقای دکتر. وقت جنابعالی بخیر.
یک سوال کلی از خدمتتان داشتم.
مفهوم سیستم های کنترل خطی چیست؟
آیا پلنت باید خطی باشد یا کنترل کننده خطی باشد؟ آیا اگر با استفاده از خطی سازی پلنت، کنترل کننده خطی طراحی کنیم، سپس سیگنال ورودی را به پلنت غیرخطی اعمال کنیم، سیستم کنترل خطی محسوب می شود؟
با سپاس از شما استاد محترم
سلام
معولا به حالتی که پلنت خطی باشه، سیستمهای کنترل خطی گفته میشه
سلام
آیا رویتگری هم وجود دارد که بتواند نسبت به نامعینی مقاوم باشد؟
برای یک سیستم که نامعینی پارامتری دارد کنترل کننده مقاوم طراحی کردم و حالا قصد دارم که از یک رویتگر برای تخمین حالت ها استفاده کنم.
سلام
تو نت سرچ کنید قطعا پیدا میشه
سلام آقای دکتر. وقت شما بخیر.
یک سوال داشتم از خدمتتان.
آیا مفهوم کلمه uncertainty با perturbation متفاوت است؟ یعنی اگر در سیستمی perturbation وجود داشته باشد، می توان تحت عنوان نامعینی در نظر گرفت؟
با سپاس
سلام
بهتره به همون مرجعی که دیدید مراجعه کنید و مفهوم کلمات رو ازش استخراج کنید.
ممکنه یه جایی این دو تا معنی یکسان داشته باشند ولی جای دیگه یکی نباشند
سلام مجدد آقای دکتر. ممنونم بابت وقتی که گذاشتید.
عذر خواهم سوال دیگری هم ازخدمتتان دارم.
در حالت کلی این دو کلمه چه تفاوتی با هم دارند؟
سپاسگزارم از شما
همونطور که گفتم به مرجع مربوطه باید مراجعه کنید
سلام – ببخشید کلا 6 مجموعه آموزش کنترل مقاوم دارید، اینها کل کنترل مقاوم دوره ارشد رو پوشش می دهند؟ البته اینکه با روش LMI است خیلی خوبه – با تشکر
سلام. بله 6 مجموعه هست ولی طبق سرفصلهای معمول که در دانشگاه تدریس میشه نیست و برای پاس کردن درس کنترل مقاوم کافی نیست.
بیشتر برای مقاله کار کردن مناسبه
سلام آقای دکتر. ممنونم بابت تدریس بی نظیرتون.
آیا استفاده از Schur complement ممکن است باعث محافظه کاری شود؟
با سپاس
سلام
خیر چون دو عبارت معادل هم هستند